高斯定理,电场与磁场的关系论述
笃信自己人在初高中的期间都练习过近于电场眼同磁场的相干常识,此中高斯定理即是此中的一个,高斯定理也好吧称为高斯公式,是一个散度的定理,高斯定律标明在合拢曲面内的电荷散步与露头的电场之间的缘由,在概的教导眼同实习方,都会触摸到电场眼同磁场的相干事故,比方说右手定律等,都是对烝黎明确电场与磁场的缘由一种至极灵验的管道,明确理会电场眼同磁场对付自己人线路地盘的缘由是对照主要的,更加是在普通的生计利用中,都必要用到这方的相干常识,日月自己人将为大众引入高斯定理眼同相干的电场、磁场缘由。
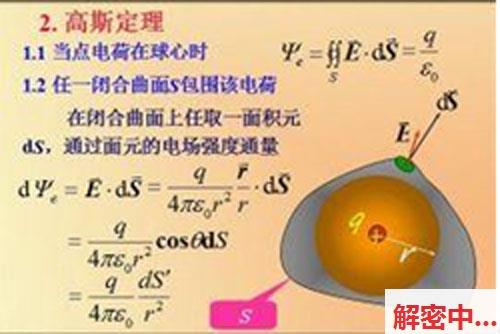
在静电学中,标明在合拢曲面内的电荷之和与露头的电场在该合拢曲面上的电通量积分之间的缘由。高斯定律标明在合拢曲面内的电荷散步与露头的电场之间的缘由。高斯定律在静电场光景下类比于利用在磁场学的安培定律,而二者都被鸠集在麦克斯韦方程组中。因为数学上的相类性,高斯定律也好吧利用于其余由反寻常定律定夺的物理量,即如引力可能辐启示。
它吐露,电场劲头对任性幽囹曲面的通量只取决于该幽囹曲面内电荷的代数和,与曲面内电荷的地位散步光景无关,与幽囹曲面外的电荷亦无关。在真空的光景下,Σq是围堵在幽囹曲面内的畅电荷的代数和。当生计介质时,Σq应明确为围堵在幽囹曲面内的畅电荷和极化电荷的总和。
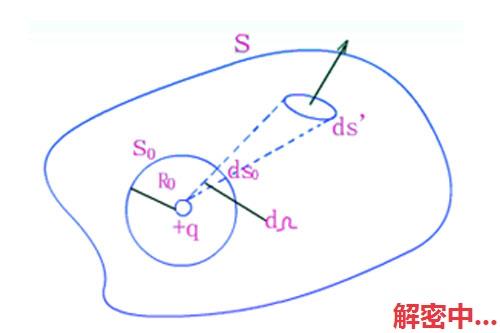
它表明电位移对任性幽囹曲面的通量只取决于曲面内畅电荷的代数,与畅电荷的散步光景无关,与极化电荷亦无关。电位移对任一面积的能量为电通量,所以电位移亦称电通密度。对付各向同性的线性的电介质,若是共计幽囹曲面S在一平均的相反介电常数为 的线性介质中,则电位移与电场劲头成正比,称为介质的相反介电常数,这是一个无穷纲的量。高斯定理在物理中的利用
揞高斯定理虽好吧将场物科学三大定律公式联合起来,但这刚刚数学式样的联合,差讹物理事理的联合,所以,高斯定理到场物科学的利用是有局限性和误导性的。高斯定理是从库伦寻常正延展定律中推导进去的,它对任何式样的寻常正延展顺序都合用,所以是一个近于场寻常正延展顺序散步的“联合”数学范式,爰也好吧看进去,不管不拘场,他们的劲头室散步数学顺序都一如,刚刚场合对应的“电荷”概区别,所以说,场领有同一性,象鍪怎样从物理事理上将区别的电荷所抖神儿的场联合起来,必要更多的通晓。
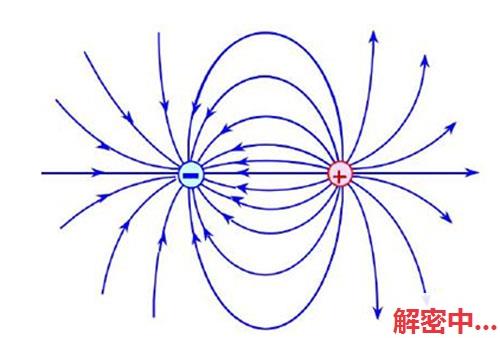
高斯定理中的密度心思劈头于光的启示,所谓启示即是点光源照射在单元面积上的光通量Φ(启示)是与漏洞R寻常成正比,如图-6所示,在个别球面上,从光源射出的光照射到球面上的面积(S)随阔别光源漏洞(R)的寻常成正比,即 ;假诺把光束数念是由自多寡的光子组的光子流,则区别R值时照射面积在拓,但每一路面积上所包孕的光子和数(Φ)是沟通的,即 =常量,ρ是曲面密度。
高斯定理把场强界说为力线通量与其垂直面积之比,实践上,高斯定理中的场强即是单元球轮廓或圆立体上的“荷”密度。佛来明右手定则
由英藉工程师佛来明所制作的定则,好吧求出指挥在磁场下挪动时所露头的电流偏向,右手三根手指相垂直,拇指的偏向是指挥挪动偏向,食指指的是磁场偏向,中指的则为电流偏向,笃信斯定则对付好多人来说都是对照理解的,因为在学徒年岁的物理教导中,就会往往着斯定则来对电场的偏向导读断定,也是最为罕用的一种方法,概自己人都略称之为右手定则,对付学徒迷漫明确电场的露头实际有很好的作态。
电场是电荷及蜕变磁场周遭室里生计的一种非凡物体。电场这种物体与一贯的件区别,它差讹由成分原子所组,但它是公平生计的,电场领有一贯物体所领有的力和能量等公平性。纳入电场中某股长的电荷受到的电场力F跟它的电量q的比值叫做该点的电场劲头,吐露该处电场的强弱。在电场中某股长弄了,则该点场强的大小与偏向即是一个定值,与纳入的检修电荷无关,哪怕不纳入检修电荷,该处的场强大小偏向仍稳固。检修电荷q充任“较量用具”的作态。
磁场蜕变时线圈露头的感生电动势与指挥的科别、体式、性子和养成均无关,是由磁场自身的蜕变肇兴的。所以麦克斯韦升起了“蜕变的磁场会在其周遭的室激起一种电场,假使这种电场使得合拢覆中露头了感生电动势和感生电流”的实际,并将这种电场称为潆电场。







